Answer:
2.5 ft
Explanation:
The figure for the given scenario is shown below.
There are two right angled triangles, ΔACD and ΔBCD
The height of flag staff is represented by segment AB, BC is the height of pedestal stand , D is a point on the ground that makes angles 30° and 60° with the bottom and top of staff at B and A respectively.
AB = 5 ft. Let the height of pedestal stand be
 ft and the distance of point D from the bottom of stand be
ft and the distance of point D from the bottom of stand be
 ft as shown in the figure.
ft as shown in the figure.
Now, from ΔACD,
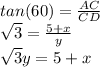
From ΔBCD,
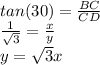
Plug in the value of
 in the first equation and solve for
in the first equation and solve for
 .
.
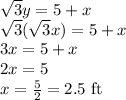 .
.
Therefore, the height of the pedestal stand is 2.5 ft.