Question

The product of two consecutive positive even numbers is 1,224. Find the numbers.

Answer 1

34 and 36.

Explanation:

By multiplying 34 by 36 (consecutive positive even numbers) we get 1,224!

Answer 2

The product of two consecutive positive even numbers is 1,224. The numbers are 34 and 36.

Solution:

Given that product of two consecutive positive even number is 1224.

Need to find the numbers

Let one even number be represented by variable x

So other consecutive even number = x + 2

As product is 1224 we can frame a equation as,

`\begin{array}{l}{\Rightarrow x(x+2)=1224} \\ {=>x^(2)+2 x=1224} \\ {=>x^(2)+2 x-1224=0}\end{array}`

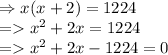
we got a quadratic equation. lets solve it by quadratic formula

According to quadratic formula for general equation a
`x^2` + bx + c = 0 , solution of the equation is given by

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

`\text { Our equation } x^(2)+2 x-1224`

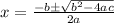
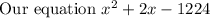
So in our case, a = 1, b = 2 and c = -1224

On applying quadratic formula we get

`\begin{array}{l}{x=\frac{-2 \pm \sqrt{2^(2)-4 * 1 *(-1224)}}{2 * 1}} \\\\ {x=(-2 \pm √(4+4896))/(2)} \\\\ {x=(-2 \pm √(4900))/(2)} \\\\ {x=(-2 \pm 70)/(2)} \\\\ {x=(68)/(2)=34 \text { or } x=(-72)/(2)=-36}\end{array}`

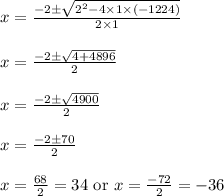
As required number is positive , ignoring the negative value

x = 34

x + 2 = 34 + 2 = 36

Hence two positive even consecutive number having product as 1224 are 34 and 36.