Answer:
85.1 m
Step-by-step explanation:
The x and y coordinates are as follows
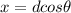
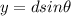 where d is distance travelled and
where d is distance travelled and
 is the slope of landing
is the slope of landing
The horizontal distance travelled is
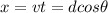 where t is time take to travel and v is the velocity
where t is time take to travel and v is the velocity
Making t the subject,

Also, the vertical distance

Therefore,
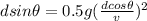 and making d the subject of the formula
and making d the subject of the formula
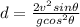
Substituting v for 20 m/s,
 for
for
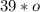 and g for
and g for
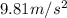

d=85.06100825
Rounding off, d=85.1 m