Answer:
0.161
Explanation:
Given:
Number of trials,
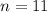
Consider the event of rolling odd number as success. There are 3 odd and 3 even numbers in a fair die.
So, probability of success,

Probability of failure,
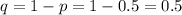
Number of successes,
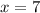
From Bernoulli's Theorem, the probability of
 successes in
successes in
 trials is given as,
trials is given as,
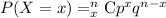
Here,
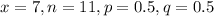
So,
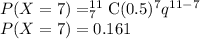
Therefore, the probability of getting an odd number exactly 7 times is 0.161.