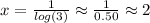Question

Explain how to solve 3x − 4 = 6 using the change of base formula log base b of y equals log y over log b. Include the solution for x in your answer. Round your answer to the nearest thousandth.

Answer 1

`x \approx 2`

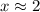
Explanation:

The given equation is

`3^(x)-4=6`

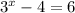
First, we move all constant terms to one side

`3^(x)=6+4\\ 3^(x)=10`

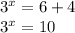
Observe that the bases are different, so first, we rewrite the expression as logarithm

`x=log_(3)(10)`

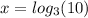
But, we need a logarithm with base 10, so we apply the following property

`log_(a)(b)=(log(b))/(log(a))`

`x=(log(10))/(log(3))`

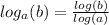
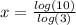
But,
`log(10)=1`

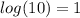
So,

`x=(1)/(log(3)) \approx (1)/(0.50) \approx 2`