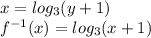Question

Write the inverse of f(x) = 3 x - 1

f -1(x) =

log3 x - 1
log3 x + 1
log3 (x - 1)

Answer 1

`f^(-1)(x)=log_3(x+1)`

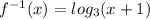
Explanation:

Function f(x) is defined as:
`f(x)=3^x-1`

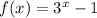
In order to find its inverse (
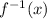`f^(-1) (x)`, we need in the first step, to replace f(x) by the variable "y":
`f(x)=3^x-1\\y=3^x-1`

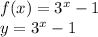
In the next step, we solve for "x" as a function of "y". Notice that we need to use the logarithm base 3 to bring the exponent "x" down:

`y=3^x-1\\y+1=3^x\\log_3(y+1)=log_3(3^x)=x\\x=log_3(y+1)`

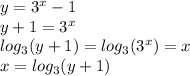
Next, we replace y with "x", and x with
`f^(-1)(x)`

`x=log_3(y+1)\\f^(-1)(x)=log_3(x+1)`