Question

Plz help me with this question

Answer 1

The equation that models the population growth is y = 90,000(1.02)^x

Explanation:

The formula of the exponential growth is y = a
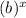`(b)^(x)`, where

• a is the initial value

• b is the factor of growth ⇒ b > 1

Let us solve the question

∵ At x = 0, the population y = 90,000

→ That means the initial value is 90,000

∴ a = 90,000

→ Substitute it in the form of the equation above

∴ y = 90,000
`(b)^(x)`

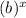
→ To find b use any values from the table to substitute x and y

∵ At x = 1, y = 91,800

∵ 91,800 = 90,000
`(b)^(1)`

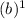
∴ 91,800 = 90,000 b

→ Divide both sides by 90,000

∵
`(91,800)/(90,000)` =
`(90,000b)/(90,000)`

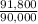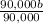
∴ 1.02 = b

→ Substitute it in the equation above

∵ y = 90,000
`(1.02)^(x)`

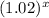
∴ The equation that models the population growth is y = 90,000(1.02)^x