Question

A batter hits a ball at 35 degrees above the horizontal and it is caught 4 seconds later 100 meters from home plate. What is the initial velocity (vector) of the ball?

Answer 1

`u=(26.5 i + 18.5j) m/s`

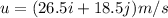
Step-by-step explanation:

The range of a projectile is given by the formula

`d=(u^2)/(g) sin 2\theta`

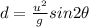
where in this case, we have

d = 100 m is the range

u is the initial speed (the magnitude of the initial velocity)

g = 9.8 m/s^2 is the acceleration of gravity

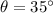`\theta = 35^(\circ)` is the angle of projection

Solving for u, we find:

`u=\sqrt{(dg)/(sin 2\theta)}=\sqrt{((100)(9.8))/(sin(2\cdot 35^(\circ)))}=32.3 m/s`

Now we can easily find the components of the initial velocity:

`u_x = u cos \theta = (32.3)(cos 35^(\circ))=26.5 m/s\\u_y = u sin \theta = (32.3)(sin 35^(\circ))=18.5 m/s`

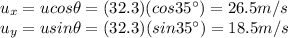
So, the initial velocity of the ball is

`u=(26.5 i + 18.5  j) m/s`

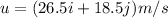
where i and j are the unit vector indicating the horizontal and vertical direction.