Question

Finding the derivative by the limit process.

f(x)=x²+x-3
f'(x)=?​

Answer 1

`\displaystyle f'(x) = 2x + 1`

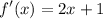
General Formulas and Concepts:

Algebra I

Terms/Coefficients

• Expanding/Factoring

Functions

• Function Notation

Calculus

Limits

Limit Rule [Variable Direct Substitution]:
`\displaystyle \lim_(x \to c) x = c`

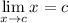
Differentiation

• Derivatives
• Derivative Notation
• Definition of a Derivative:
  `\displaystyle f'(x) = \lim_(h \to 0) (f(x + h) - f(x))/(h)`

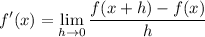
Explanation:

Step 1: Define

Identify

`f(x) = x^2 + x - 3`

Step 2: Differentiate

1. Substitute in function [Definition of a Derivative]:
   `\displaystyle f'(x) = \lim_(h \to 0) ([(x + h)^2 + (x + h) - 3] - (x^2 + x - 3))/(h)`
2. Expand:
   `\displaystyle f'(x) = \lim_(h \to 0) (x^2 + 2hx + h^2 + x + h - 3 - x^2 - x + 3)/(h)`
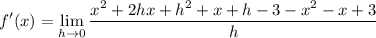
3. Combine like terms:
   `\displaystyle f'(x) = \lim_(h \to 0) (2hx + h^2 + h)/(h)`
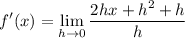
4. Factor:
   `\displaystyle f'(x) = \lim_(h \to 0) (h(2x + h + 1))/(h)`
5. Simplify:
   `\displaystyle f'(x) = \lim_(h \to 0) 2x + h + 1`
6. Evaluate [Limit Rule - Variable Direct Substitution]:
   `\displaystyle f'(x) = 2x + 0 + 1`
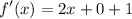
7. Simplify:
   `\displaystyle f'(x) = 2x + 1`

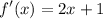
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation