Answer:
B. 12
Explanation:
✔️Find the value of x
The side lengths of two similar triangles are always proportional.
Given that ∆ABC ~ ∆LMN, therefore:
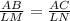
AB = 5
LM = 10
AC = x + 5
LN = 3x + 3
Plug in the values
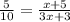
Cross multiply
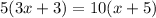
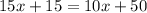 (distributive property)
(distributive property)
Collect like terms
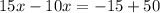
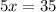
Divide both sides by 5
x = 7
✔️Find AC
AC = x + 5
Plug in the value of x
AC = 7 + 5
AC = 12