The function that has a range of y<3 is y=-(2)* + 3
Answer: Option(c)
Explanation:
Solution:
Lets shall evaluate the options given in the question
In Option 1; y=3(2) that is
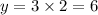
So the value of y>3 and thus option 1 fails
In option 2; y=2(3)*
This expression indicates that the power of 3 all result in positive values and sometimes zero such that for
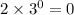 and for values other than one y will be greater than 3. so option 2 fails.
and for values other than one y will be greater than 3. so option 2 fails.
In option 4; y=2x(-3)
On solving we get
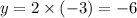
Though it is less than 3 but it has an negative value. So option 4 fails.
In option 3; y=-(2)* + 3
This option indicates for all power values of -2 the y value will be less than 3 such that
For power value 0 we get
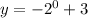
y=0+3=3
And for the power value 1 we get
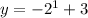
y=-2+3=1
So in the both the occasion the value of y<3 than and it is not an negative value and thus option 3 satisfy the functional range y<3.
Result:
Thus the function that has a range of y<3 is y=-(2)* + 3