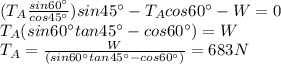Question

What is the tension in cord A in this diagram? It would help if you answered in Newtons but not absolutely necessary. I know the answer already (683 N) I would just like to see how to get to the answer

Answer 1

683 N

Step-by-step explanation:

If the block is in equilibrium, then the net force acting on it is zero.

We have therefore to resolve each force along the x- and y- direction, and equate the net force along each direction to zero. Doing so, we obtain the following equations:

`T_B cos 45^(\circ) - T_A sin 60^(\circ) = 0\\T_B sin 45^(\circ) - T_A cos 60^(\circ) - W = 0`

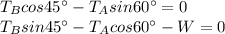
where

`T_A` is the tension in cord A

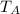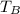`T_B` is the tension in cord B

W = 250 N is the weight of the block

From the first equation we get:

`T_B = T_A (sin 60^(\circ))/(cos 45^(\circ))`

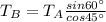
And substituting into the second equation, we find the tension in cord A:

`(T_A (sin 60^(\circ))/(cos 45^(\circ))) sin 45^(\circ) - T_A cos 60^(\circ) - W = 0\\T_A (sin 60^(\circ) tan 45^(\circ) - cos 60^(\circ)) = W\\T_A=(W)/( (sin 60^(\circ) tan 45^(\circ) - cos 60^(\circ)))=683 N`