Question

How to solve these two questions? ​

Answer 1

1) See attached figure

The relationship between charge and current is:

`i = (Q)/(t)`

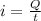
where

i is the current

Q is the charge

t is the time

Therefore, the current is the rate of change of the charge passing through a given point over time.

This means that for a graph of charge over time, the current is just equal to the slope of the graph.

For the graph in this problem:

- Between t = 0 and t = 2 s, the slope is

`(50-0)/(2-0)=25 C/s`

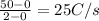
therefore the current is

i = 25 A

- Between t = 2 s and t = 6 s, the slope is

`(-50-(50))/(6-2)=-25 C/s`

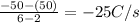
therefore the current is

i = -25 A

- Between t = 6 s and t = 8 s, the slope is

`(0-(-50))/(8-6)=25 C/s`

therefore the current is

i = 25 A

The figure attached show these values plotted on a graph.

2)
`15 \mu C`

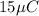
The previous equation can be rewritten as

`Q = i t`

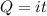
This equation is valid if the current is constant: if the current is not constant, then the total charge is simply equal to the area under a current vs time graph.

Here we have the current vs time graph, so we gave to find the area under it.

The area of the first triangle is:

`A_1 = (1)/(2)(0.001 s)(0.010 A)=5\cdot 10^(-6) C`

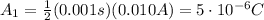
While the area of the second square is

`A_2 = (0.002 s - 0.001 s)(0.010 A)=1\cdot 10^(-5)C`

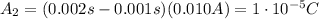
So, the total area (and the total charge) is

`Q=A_1 +A_2 = 5\cdot 10^(-6) + 1\cdot 10^(-5) = 1.5\cdot 10^(-5)C=1.5 \mu C`