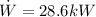Question

Windmills slow the air and cause it to fill a larger channel as it passes through the blades. Consider a circular windmill with a D1 = 8m diameter rotor in a V1 = 12m/s wind. The wind speed after the windmill is measured at 8 m/s. (a) (7 pt) Determine the diameter of the wind channel downstream from the rotor (D2). (b) (8 pt) Calculate the power produced by this windmill in kW. Assume air is incompressible and use air density of 1.2kg/m3 .

Answer 1

DIAMETER = 9.797 m

POWER =
`\dot W = 28.6 kW`

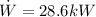
Step-by-step explanation:

Given data:

circular windmill diamter D1 = 8m

v1 = 12 m/s

wind speed = 8 m/s

we know that specific volume is given as

`v =(RT)/(P)`

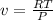
where v is specific volume of air

considering air pressure is 100 kPa and temperature 20 degree celcius

`v =  (0.287* 293)/(100)`

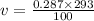
v = 0.8409 m^3/ kg

from continuity equation

`A_1 V_1 = A_2 V_2`

`(\pi)/(4)D_1^2 V_1 = (\pi)/(4)D_1^2 V_2`

`D_2 = D_1 \sqrt{(V_1)/(V_2)}`

`D_2 = 8 * \sqrt{(12)/(8)}`

`D_2 = 9.797 m`

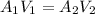
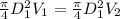
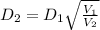
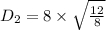
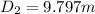
mass flow rate is given as

`\dot m = (A_1 V_1)/(v) = (\pi 8^2* 12)/(4* 0.8049)`

`\dot m = 717.309 kg/s`

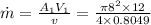
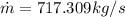
the power produced
`\dot W = \dot m ( V_1^2 - V_2^2)/(2) = 717.3009 [(12^2 - 8^2)/(2) * (1 kJ/kg)/(1000 m^2/s^2)]`

`\dot W = 28.6 kW`