Answer: 75.9%
Explanation:
Given : Number of cans bought by Karen : n=23
Proportion of cans sold at that particular grocery store are dented : p= 0.06
We assume that the store's inventory is large enough that no individual customer's purchase affects the dent rate for the remaining cans.
Let x be binomial variable that represents the dented can.
Using binomial probability formula ,
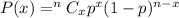
The probability that Karen has bought at least one dented can:-

Hence, the required probability = 75.9%