Question

Oops, you were just caught for running a red light by the interstellar police. In your defense, you argue with the officer that the light appeared to be green though he insists that from his vantage point standing still relative to the signal, the light was steadily red when you barreled through the intersection. How fast were you approaching the light so that it appeared green to you, while red to the officer? HINT 1: Look up and note in your answer the wavelengths that correspond to red and green ligh

Answer 1

`v=6.04*10^7(m)/(s)`

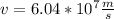
Step-by-step explanation:

The change in the wavelength observed due to the relativistic doppler effect when the source approaches is given by the following expression:

`\lambda_e=\lambda_o\frac{\sqrt{1+(v)/(c)}}{\sqrt{1-(v)/(c)}}`

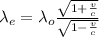
Here,
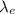`\lambda_e` is the emmited wavelength (red),
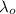`\lambda_o` is the observed wavelength (green) and v is the approaching speed. So,
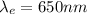`\lambda_e=650nm` and
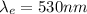`\lambda_e=530nm`. Solving for v:

`(\lambda_e)/(\lambda_o)=\frac{\sqrt{1+(v)/(c)}}{\sqrt{1-(v)/(c)}}\\(\lambda_e^2)/(\lambda_o^2)=\frac{1+(v)/(c)}{{1-(v)/(c)}}\\\\(1-(v)/(c))(\lambda_e^2)/(\lambda_o^2)=1+(v)/(c)\\(\lambda_e^2)/(\lambda_o^2)-(v\lambda_e^2)/(c\lambda_o^2)=1+(v)/(c)\\(v)/(c)+(v\lambda_e^2)/(c\lambda_o^2)=(\lambda_e^2)/(\lambda_o^2)-1\\v((1)/(c)+(\lambda_e^2)/(c\lambda_o^2))=(\lambda_e^2)/(\lambda_o^2)-1\\`

`v=((\lambda_e^2)/(\lambda_o^2)-1)/((1)/(c)+(\lambda_e^2)/(c\lambda_o^2))\\v=((\lambda_e^2)/(\lambda_o^2)-1)/((1)/(c)(1+(\lambda_e^2)/(\lambda_o^2)))`

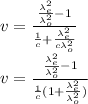
Recall that
`c=3*10^8(m)/(s)`, replacing this and the wavelengths:

`v=(((650nm)^2)/((530nm)^2)-1)/((1)/(3*10^8(m)/(s))(1+((650nm)^2)/((530nm)^2)))\\\\v=6.04*10^7(m)/(s)`

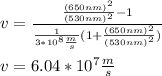
This is the incredible speed at which you would have to be moving to see the red light as green light.