Question

Assume that the die is weighted so that the probability of a 1 is 0.1, the probability of a 2 is 0.2, the probability of a 3 is 0.1, the probability of a 4 is 0.2, the probability of a 5 is 0.1, and the probability of a 6 is 0.3. You roll the die until the sum of all numbers which have appeared exceeds 3. A random variable X is defined to be the number of rolls. Outcomes of X are 1, 2, 3, 4.

What are the probabilities of each outcome?

Answer 1

The probabilities of each outcome are the following:

for X = 1 is 0.6

for X = 2 is 0.35

for X = 3 is 0.049

and for X = 4 is 0.001

Explanation:

Let's consider X as the random variable for the sum of outcomes "S" exceeds 3, this is:
`S\geq 4`

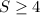
Let's now analyze and consider the ways that X equals the different values:

X = 1: I throw the dice and the result is: 4, 5 and 6.

Then: P(X=1) = P(4) + P(5) + P(6) = 0.2+0.1+0.3 = 0.6

Thus P(X=1) = 0.6

X = 2: The result after following the dice two times can be:

1 and 3, 1 an 4.... and so on until 1 and 6

2 and 2, 2 and 3... and so on until 2 and 6

3 and 1... and so on until 3 a 6

Then P(X=2) = P(1)xP(3,4,5,6) + P(2)xP(2....6) + P(3)x(1.....6)

Theory of Probability: Sum of all possible outcomes P(1)+P(2).......P(6) = 1

Then P(1......6) = 1

Then P(X=2) = P(1)x[1-P(1)-P(2)]+P(2)x[1-P(1)]+P(3) = 0.1x(1-0.1-0.2) + 0.2x(1-0.1) + 0.1 = 0.1 x 0.7 + 0.2 x 0.9 + 0.1 = 0.35

Thus P(X=2) = 0.35

X = 3: The result can be

1 and 1 and 2, 1 and 1 and 3.... until 1 and 1 and 6

1 and 2 and 1, 1 and 2 and 2..... until 1 and 2 and 6

2 and 1 and 1, 2 and 1 and 2.... until 2 and 1 and 6

Then P(X=3) = P(1)xP(1)xP(2....6) + P(1)xP(2)xP(1.....6) + P(1)xP(2)xP(1.....6)

P(X=3) = 0.1 x 0.1 x (1-0.1) + 0.1 x 0.2 x 1 + 0.2 x 0.1 x 1 = 0.01 x 0.9 + 0.2 + 0.2 = 0.049

Thus P(X=3) = 0.049

Finally, for X to be 4, I only have the following possibilities

1 and 1 and 1 and 1.... until 1 and 1 and 1 and 6

Then P(X=4) = P(1)xP(1)xP(1)xP(1.....6) = 0.1x0.1x0.1x1 = 0.001

Thus P(X=3) = 0.001