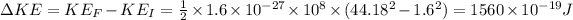Answer:
(A) Speed will be
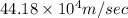
(b) Change in kinetic energy =
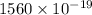
Step-by-step explanation:
We have given mass of proton

Acceleration of the proton
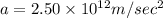
Initial velocity u =
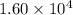 m/sec
m/sec
Distance traveled by proton s = 3.90 cm = 0.039 m
(a) From third equation of motion we know that

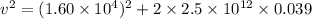
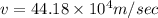
(b) Initial kinetic energy
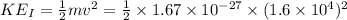
Final kinetic energy
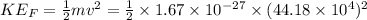
So change in kinetic energy