Question

The speed limit on a road is 60 mph. The actual speeds of cars are measured and found to be normally distributed with a mean value of 63 mph and a standard deviation of 5 mph. Approximately what percentage of cars exceed the speed limit by more than 10 mph?

A) 5.0%
B) 6296%
C) 7.3%
D) 8.1%

Answer 1

Answer: 8.1%

Explanation:

Given :
`\mu=63`

`\sigma=5`

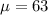
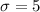
Let x be the random variable that represents the actual speeds of cars.

The speed limit on a road is 60 mph.

Using formula ,
`z=(x-\mu)/(\sigma)`, we have for x= 60+10=70

`(70-63)/(5)=1.4`

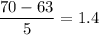
Using z-table for right-tailed test value, The probability of cars exceed the speed limit by more than 10 mph will be

`P(x>70)=P(z>1.4)=0.0807567\approx0.081=8.1\%`

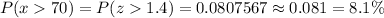
Hence, the percentage of cars exceed the speed limit by more than 10 mph is 8.1%.