Question

Three variables N, D, and Y , all have zero sample means and unit sample variances. A fourth variable is C = N + D. In the regression of C on Y , the slope is 0.8. In the regression of C on N, the slope is 0.5. In the regression of D on Y the slope is 0.4. What is the error sum of squares in the regression of C on D? There are 21 observations.

Answer 1

Error sum of squares SSE = 15

Explanation:

Given:

C = N + D

Var C = Var N + Var D + 2 Cov(N,D)

= 2(1+ Cov(N,D))

from 2 simple regreesion

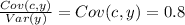`(Cov(c,y))/(Var(y)) = Cov(c,y) = 0.8` however

Cov(c,y) = Cov(N + D, y) = Cov(N,y) + Cov(D,y)

AND

Cov(C,N) =Cov(N + D, N) = Var N + Cov(D,N) = 0.5

Cov(D,N) = -0.5

therefore

Var(C) = 2(1-0.5) = 1

ALSO

Cov(C,D) = Cov( N+D,D)

= Cov( N,D) + Var(D)

= -0.5 + 1 = 0.5

Slope of C on D =
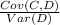`(Cov(C,D))/(Var(D))`= 0.5

finaly we have

Error sum of square (SSE) = SST -SSR

= (n-1) Sc^2 - slope^2(n-1) Sd^2

=20(1)^2 - 0.5^2(20)(1)

SSE = 15