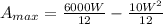Question

A rectangular field will be fenced on all four sides. Fencing for the north and south sides costs $6 per foot and fencing for the other two sides costs $5 per foot. What is the maximum area that can be included for $6000

Answer 1

The maximum area that can be included for $6000 is
`A_(max)=75000 \:{ft^(2)}`

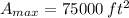
Explanation:

We can use the fact that the area of a rectangular field is given by the formula

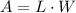`A=L\cdot W` where

`L` = length of the field

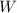`W` = the width of the field

From the information given the total cost of rectangular field is

`\$6000=2\cdot \$6 \cdot L+2\cdot \$5\cdot W\\\$6000=\$12 \cdot L+\$10\cdot W`

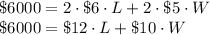
From the area formula we can say
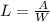`L=(A)/(W)` and substitute into the total area cost as follows:

`\$6000=\$12 \cdot ((A)/(W) )+\$10\cdot W`

And we solve for A, which is the maximum area

`\$6000=\$12 \cdot ((A)/(W) )+\$10\cdot W\\12\cdot (A)/(W)+10W-10W=6000-10W\\12\cdot (A)/(W)=6000-10W\\(12A)/(W)W=6000W-10WW\\(12A)/(12)=(6000W)/(12)-(10W^2)/(12)\\A_(max)=(6000W)/(12)-(10W^2)/(12)`

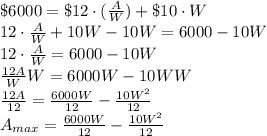
The equation we obtain is a parabola, for this reason we need to find the W-coordinate of the vertex.

`W=-(b)/(2a)`

`W=-((6000)/(12) )/(2(-(10)/(12) ))\\W=300`

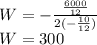
and since

`A_(max)=(6000W)/(12)-(10W^2)/(12)`

`A_(max)=(6000(300))/(12)-(10(300)^2)/(12)\\A_(max)=75000 \:{ft^(2)}`