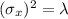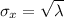Question

Geologists estimate the time since the most recent cooling of a mineral by counting the number of uranium fission tracks on the surface of the mineral. A certain mineral specimen is of such an age that there should be an average of 6 tracks per cm2 of surface area. Assume the number of tracks in an area follows a Poisson distribution. Let X represent the number of tracks counted in 1 cm2 of surface area.

a)Find P(X = 7).

b)Find P(X ≥ 3).

c)Find P(2 < X < 7).

d)Find μX.

e)Find σX

Answer 1

The required answer is shown below:

Explanation:

Consider the provided information.

The formula for calculating poisson probability mass function:
`P(k)=(\lambda^ke^(-\lambda) )/(k!)`

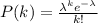
Where λ is average number of events, the value of e = 2.718..

K can take the values 0,1,2...

Part (a)Find P(X = 7).

A certain mineral specimen is of such an age that there should be an average of 6 tracks per cm² of surface area.

Use the above formula and substitute x=7 and λ=6

`P(X=7)=(6^7e^(-6) )/(7!)`

`P(X=7)=0.1377`

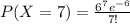
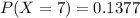
Hence, P(X = 7) = 0.1377

Part (b)Find P(X ≥ 3).

This can be calculated as:

`P(X\geq 3)=1-P(X=0)-P(X=1)-P(X=2)`

`P(X\geq 3)=1-(6^0e^(-6) )/(0!)-(6^1e^(-6))/(1!)-(6^2e^(-6))/(2!)`

`P(X=7)=0.9380`

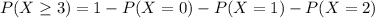
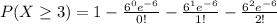
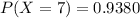
Hence, P(X ≥ 3) = 0.9380

Part (c)Find P(2 < X < 7).

The sum can be calculated as:

`P(2<X<7)=P(X=3)+P(X=4)+P(X=5)+P(X=6)`

`P(2<X<7)=(6^3e^(-6) )/(3!)+(6^4e^(-6))/(4!)+(6^5e^(-6))/(5!)+(6^6e^(-6))/(6!)`

`P(2<X<7)=0.5443`

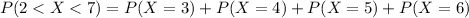
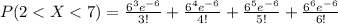
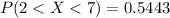
Hence, P(2 < X < 7)= 0.5443

Part (d)Find μX.

If λ is average number of successes or region in the Poisson distribution, then the mean and the variance of the Poisson distribution are both equal to λ.

`\mu_x=\lambda=6`

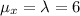
Part (e)Find σX

If λ is average number of successes or region in the Poisson distribution, then the mean and the variance of the Poisson distribution are both equal to λ.

`(\sigma_x)^2=\lambda`

`\sigma_x=√(\lambda)`

`\sigma_x=√(6)=2.449`