Question

The temperature function (in degrees Fahrenheit) in a three dimensional space is given by T(x, y, z) = 3x + 6y - 6z + 1. A bee is constrained to live on a sphere of radius 3 centered at the origin. In other words, the bee cannot fly off of this sphere. What is the coldest temperature that the bee can experience on this sphere? Where does this occur? What is the hottest temperature that the bee can experience on this sphere? Where does this occur?

Answer 1

You're looking for the extreme values of
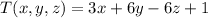`T(x,y,z)=3x+6y-6z+1` subject to
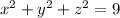`x^2+y^2+z^2=9`. The Lagrangian is

`L(x,y,z,\lambda)=3x+6y-6z+1+\lambda(x^2+y^2+z^2-9)`

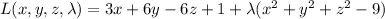
with critical wherever the partial derivatives vanish:

`L_x=3+2\lambda x=0\implies x=-\frac3{2\lambda}`

`L_y=6+2\lambda y=0\implies y=-\frac3\lambda`

`L_z=-6+2\lambda z=0\implies z=\frac3\lambda`

`L_\lambda=x^2+y^2+z^2-9=0`

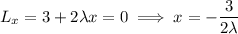
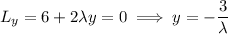
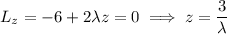
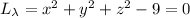
Substituting the first three solutions into the last equation gives

`\frac9{4\lambda^2}+\frac9{\lambda^2}+\frac9{\lambda^2}=9`

`\implies\lambda=\pm\frac32`

`\implies x=1,y=2,z=-2\text{ or }x=-1,y=-2,z=2`

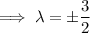
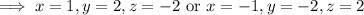
At these points, we have

`T(1,2,-2)=28`

`T(-1,-2,2)=-26`

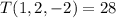
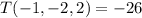
so the highest temperature the bee can experience is 28º F at the point (1, 2, -2), and the lowest is -26º F at the point (-1, -2, 2).