Answer:
2h / 3
Step-by-step explanation:
Let after time t , collision occurs
distance covered by A
= 1/2gt²
Let u be the initial velocity with which B was thrown upwards
distance by B
= ut - 1/2 gt²
total distance by A and B
h = ut - 1/2 gt² + 1/2gt²
h = ut
t = h / u
velocity of A after t
= gt
= g x h/u
velocity of B after t
= u - gt
= u - g x h/u
given
g x h/u = 2 (u - g x h/u)
2u² - 2gh = gh
u =
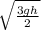
t = h / u
=
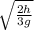
Distance covered by A
= 1/2 gt²
= 1/2 x 2h/3
= h/3
Height at which collision occured
= h - h/3
= 2h /3