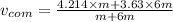Answer:
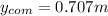

Step-by-step explanation:
Given
first stone mass is m
second stone mass is 6 m
distance traveled by first stone in 430 ms
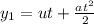
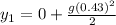
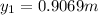
Distance traveled by stone 2 in t=430-59=371 ms
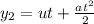
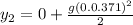
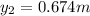
velocity of first stone after t=0.43 s
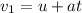
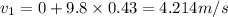
velocity of second stone after t=0.371 s

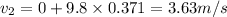
Position of Center of mass of system

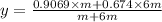

Velocity of COM