Question

A long, straight wire is surrounded by a hollow metal cylinder whose axis coincides with that of the wire. The wire has a charge per unit length of λ, and the cylinder has a net charge per unit length of 2λ. From this information, use Gauss's law to find the following. (Use lambda for λ, epsilon_0 for ε0, and r for r as necessary.)

(a) the charge per unit length on the inner and outer surfaces of the cylinder
______________(inner surface)

______________(outer surface)

(b) the electric field outside the cylinder, a distance r from the axis
______________

Answer 1

Step-by-step explanation:

It is given that, a long, straight wire is surrounded by a hollow metal cylinder whose axis coincides with that of the wire.

The charge per unit length of the wire is
`\lambda` and the net charge per unit length is
`2 \lambda`.

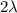We know that there exist zero electric field inside the metal cylinder.

(a) Using Gauss's law to find the charge per unit length on the inner and outer surfaces of the cylinder. Let
`\lambda_i\ and\ \lambda_o` are the charge per unit length on the inner and outer surfaces of the cylinder.

For inner surface,

`\phi=(q_(enclosed))/(\epsilon_o)`

`E.A=(q_(enclosed))/(\epsilon_o)`

`0=(\lambda_i+\lambda)/(\epsilon_o)`

`\lambda_i=-\lambda`

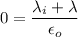
For outer surface,

`\lambda_i+\lambda_o=2\lambda`

`-\lambda+\lambda_o=2\lambda`

`\lambda_o=3\lambda`

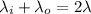
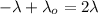
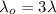
(b) Let E is the electric field outside the cylinder, a distance r from the axis. It is given by :

`E_o=(\lambda_o)/(2\pi \epsilon_o r)`

`E_o=(3\lambda)/(2\pi \epsilon_o r)`

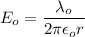
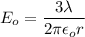
Hence, this is the required solution.