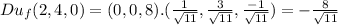Answer:
a)
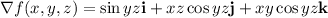 .
.
b)

Explanation:
Given a function
 , this function has the following gradient:
, this function has the following gradient:
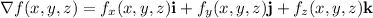 .
.
(a) find the gradient of f
We have that
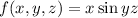 . So
. So
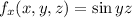
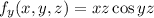
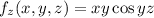 .
.
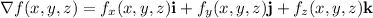 .
.
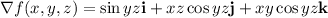
(b) find the directional derivative of f at (2, 4, 0) in the direction of v = i + 3j − k.
The directional derivate is the scalar product between the gradient at (2,4,0) and the unit vector of v.
We have that:
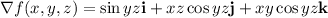
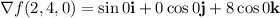 .
.
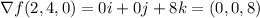
The vector is
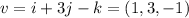
To use v as an unitary vector, we divide each component of v by the norm of v.
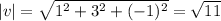
So
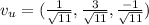
Now, we can calculate the scalar product that is the directional derivative.