Question

A baseball diamond is a square with side 90 ft. A batter hits the ball and runs toward first base with a speed of 26 ft/s.

(a) At what rate is his distance from second base decreasing when he is halfway to first base?
ft/s
(b) At what rate is his distance from third base increasing at the same moment?
ft/s

Answer 1

(a) Distance decreases at a rate of 11.628 ft/s.

(b) Distance increases at a rate of 11.628 ft/s.

Explanation:

Refer to the diagram attached to at the bottom of this answer. We will call a the distance between the batter and 1st base, x the distance between the batter and 2nd base and y the distance between the batter and 3rd base.

The speed of the batter toward first base is 26 ft/s, which means:

`(da)/(dt)=26ft/s`

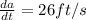
Since the diamond is a square, the angle between trajectories in each base is a square angle, so we can use Pythagoras theorem:

`x=√(90^2+(90-a)^2)`

`x=√(a^2-180a+16200)`

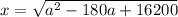
Finding the first derivative:

`(dx)/(dt)=(a-90)/(√(a^2-180a+16200))(da)/(dt)`

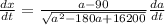
When the batter is halfway to 1st, a = 45 ft, then:

`(dx)/(dt)=(45-90)/(√(45^2-(180)(45)+16200))26=-(26)/(\sqrt5)=-11.628ft/s`

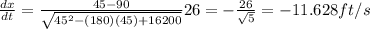
So the distance between the batter and 2nd base decreases at 11.628 ft/s

Now, using Pythagoras again to find y:

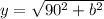`y=√(90^2+b^2)` and we know that
`(db)/(dt)=26ft/s`

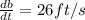
Finding the first derivative:

`(dy)/(dt)=(b)/(√(b^2+8100))(db)/(dt)`

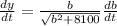
at b = 45 ft

`(dy)/(dt)=(45)/(√(45^2+8100))26=(26)/(\sqrt5)=11.628ft/s`

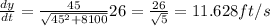
So the distance between the batter and 3rd base increases at 11.628 ft/s