Question

A survey is being planned to determine the mean amount of time corporation executives watch television. A pilot survey indicated that the mean time per week is 12 hours, with a standard deviation of 3 hours. It is desired to estimate the mean viewing time within one quarter hour. The 0.95 degree of confidence is to be used. How many executives should be surveyed?

Answer 1

Answer: 554

Explanation:

Formula we use to find the sample size :

`n=((z_(\alpha/2)\cdot\sigma)/(E))^2`

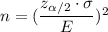
Given : Standard deviation :
`\sigma=3\ hour`

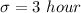
Margin of error : E=one quarter hour = 0.25 hour

Two-tailed , Critical value use for 0.95 degree of confidence:
`z_(\alpha/2)=1.96`

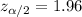
i.e.
`n=(((1.96)\cdot(3))/(0.25))^2=553.1904\approx554`

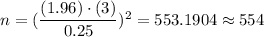
Hence, the required sample size = 554

i.e. 554 executives should be surveyed.