Question

You own a bond with a par value of $1,000 and a coupon rate of 8.50% (semiannual coupon). You know it has a current yield of 7.00%. What is its yield to maturity? The bond has 6 years to maturity. Current Yield = (annual payment / price). (hint: solve for price to answer the question). The answer is 4.40% but i dont know how to get that answer. I have a HP 10bll + Financial Calculator but i dont know how to put this into the calculator

Answer 1

YTM = 4.40%

Step-by-step explanation:

From current yield we solve for price:

current yield: annual payment/ price

0.07 = 1,000 x 8.5% / price

85 / 0.07 = price = 1214,285714285714 = 1214.29

Now we solve for yield to maturity. This is the rate at which the present value value of the maturity and coupon payment are equal to his current price:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 42.50

time 12 (6 years x 2 payment per year)

rate (semiannual as the payment are twice per year)

`42.5 * (1-(1+r)^(-12) )/(r) = PV\\`

PV coupon

`(Maturity)/((1 + rate)^(time) ) = PV`

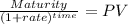
Maturity 1,000.00

time 12.00

rate

`(1000)/((1 +r)^(12) ) = PV`

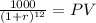
PVmaturity

PV c + PV m = $1,214.2903

So we got:

`42.5 * (1-(1+r)^(-12) )/(r) + (1000)/((1 +r)^(12) )= 1,214.2903`

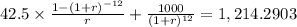
From here we solve using excel or financial calculator as you suggest.

notice this will give you the semiannual rate: 0.021988524 = 2.20%

You will have to multiply the answer by 2 giving you the 4.40% as you were told.