Step-by-step explanation:
The reaction is as follows.
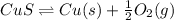
As, value of
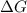 is positive. Therefore, reaction is non-spontaneous.
is positive. Therefore, reaction is non-spontaneous.
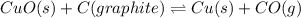
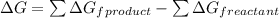
= [-137.2 - (127.2 kJ/mol)]
= -10 kJ/mol
Since, value of
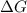 is negative here so, reaction is spontaneous.
is negative here so, reaction is spontaneous.
Also,
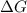 = -RT ln
= -RT ln
where, R = 8.314 J/mol K
T =
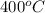 = (400 + 273) K = 673 K
= (400 + 273) K = 673 K
K = equilibrium constant
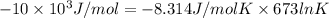
100 =
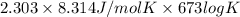
log K = 0.00776
K = 1.018
Therefore, we can conclude that equilibrium constant for the coupled reaction is 1.018.