Question

A business executive, transferred from Chicago to Atlanta, needs to sell her house in Chicago quickly. From conversations with her realtor, the executive believes the price she will get by leaving the house on the market for another month is uniformly distributed between $203,000 and $239,000. If she leaves the house on the market for another month, what is the probability that she will get less than $222,000?

Answer 1

There is a 52.78% probability that she will get less than $222,000.

Step-by-step explanation:

An uniform probability is a case of probability in which each outcome is equally as likely.

For this situation, we have a lower limit of the distribution that we call
`a` and an upper limit that we call
`b`.

The probability that we find a value X lower than x is given by the following formula.

`P(X \leq x) = (x - a)/(b-a)`

For this problem, we have that:

Uniformly distributed between $203,000 and $239,000, so
`b = 239,000, a = 203,000`.

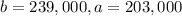What is the probability that she will get less than $222,000?

So
`x = 222,000`

`P(X \leq x) = (x - a)/(b-a)`

`P(X \leq 222,000) = (222,000 - 203,000)/(238,000-203,000) = 0.5278`

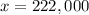
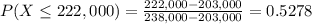
There is a 52.78% probability that she will get less than $222,000.