Answer:
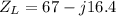 Ω
Ω
Step-by-step explanation:
Given that
d(min,0)= 4 cm
d(min,1)= 14 cm
Voltage standingwave ratio = 1.5
Zo = 50 Ω
We know that
d(min,1) - d(min,0) = λ/2
Now by putting the values
14 - 4 = λ/2
λ = 20 cm
We also know that
β=2π/λ
β=2π/0.2 = 10π rad/m
So we can say that
θr= 2β d(min,n) - (2 n + 1)π rad
θr=2×10π ×0.04 −π = -0.2 π rad
We know that
π rad = 180 °
θr= = -0.2 π rad= -36 °
We know that
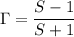
Here S= 1.5
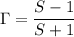
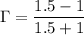
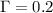
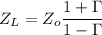
by putting the values
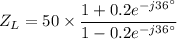
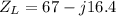 Ω
Ω