Question

According to the "January theory," if the stock market is up for the month of January, it will be up for the year. If it is down in January, it will be down for the year. According to an article in The Wall Street Journal, this theory held for 25 out of the last 34 years. Suppose there is no truth to this theory; that is, the probability it is either up or down is 0.5.

What is the probability this could occur by chance? (Round your answer to 6 decimal places.)

Answer 1

The probability this could occur by chance is approximately 0.003053.

Explanation:

This problem can be solved with a binomial distribution, if we imagine that by the end of January the stock market will follow the same pattern for the rest of the year we can define the following random variable:

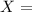`X =` "The stock market will be up for the rest of the year",

and
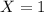`X = 1` if by the end of January the stock market is up and
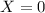`X = 0` otherwise, this way
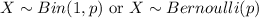`X \sim Bin(1,p) \text{ or } X \sim Bernoulli(p)`, where p is the probability of success. Next we can define the following random variable:

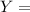`Y =` "Sum of all years where the stock market was up"

Now, the sum of a Bernoulli random variables is a Binomial random variable, in other words
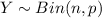`Y \sim Bin(n,p)`, where n is the number of trials and p is the probability of success. The pdf of Y is given by:

`P(X = k) = \big {n \choose k}p^k(1-p)^(n-k), \text{ } k \leq n`

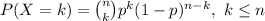
The question give us the
`n = 34`,
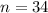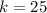`k = 25` and
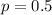`p = 0.5`. Now we just have to solve it:

`P(X = 25) = \big {34 \choose 25}(0.5)^(25)(1-0.5)^(34-25) = {34 \choose 25}(0.5)^(34) = \\P(X = 25)= 52451256\cdot(0.5)^(34) \approx 0.003053`

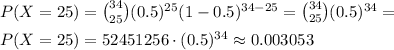
Which is highly unlikely to happen.