Question

In ∆MNP, m∠N = 90º, NH – altitude, m∠P = 21º, PM = 4 cm. Find MH.

Answer 1

0.51 cm

Explanation:

In right triangle MNP, MP = 4 cm, m∠N = 90°, m∠P = 21°

By the sine definition,

`\sin \angle P=\frac{\text{Opposite leg}}{\text{Hypotenuse}}=(MN)/(MP)\\ \\MN=MP\sin \angle P\\ \\MN=4\sin 21^(\circ)\approx 1.43\ cm`

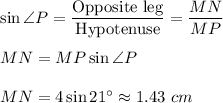
Now, consider right triangle HMN (it is right because NH is an altitude). By the cosine definition,

`\cos \angle M=\frac{\text{Adjacent leg}}{\text{Hypotenuse}}=(MH)/(MN)\\ \\MH=MN\cos \angle M`

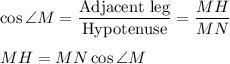
In the right triangle, two acute angles are always complementary, so

`m\angle M=90^(\circ)-m\angle P=90^(\circ)-21^(\circ)=69^(\circ)`

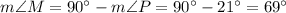
Thus,

`MH=1.43\cos 69^(\circ)\approx 0.51\ cm`