Question

Keith is a drummer who purchases his drumsticks online. When practicing with the newest pair, he notices they feel heavier than usual. When he weighs one of the sticks, he finds that it is 2.23 oz. The manufacturer's website states that the average weight of each stick is 1.85 oz with a standard deviation of 0.18 oz. Assume that the weight of the drumsticks is normally distributed.

What is the probability of the stick's weight being 2.23 oz or greater? Give your answer as a percentage precise to at least two decimal places.

Answer 1

Answer: 0.0174

Explanation:

Given :
`\mu=1.85\ \ ; \sigma=0.18`

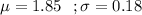
Let x be the random variable that represents the weight of the drumsticks.

We assume that the weight of the drumsticks is normally distributed.

Now, the z-score for x=2.23 ,
`\because z=(x-\mu)/(\sigma)`

`\Rightarrow\ z=(2.23-1.85)/(0.18)\approx2.11\ \ \`

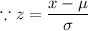
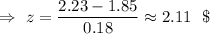
Using z-value table , we have

P-value =P(x≥2.23)=P(z≥2.11)=1-P(z<2.11)=1-0.9825708

=0.0174292≈0.0174 [Rounded nearest 4 decimal places]

Hence, the probability of the stick's weight being 2.23 oz or greater = 0.0174