The runner's Achilles tendon will stretch by approximately
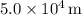 when subjected to a force 8.0 times the runner's weight. This corresponds to about
when subjected to a force 8.0 times the runner's weight. This corresponds to about
 times the tendon's original length.
times the tendon's original length.
To calculate the stretch of the Achilles tendon, we can use Hooke's Law, which states that the force applied to a spring or elastic material is proportional to the resulting displacement.
Hooke's Law is given by the formula:
![\[ F = (\Delta L)/(L_0) \cdot Y \cdot A \]](https://img.qammunity.org/2020/formulas/physics/high-school/fmey0js29w2h7aj28rs81tziyjltfgk8j8.png)
where:
- F is the force applied,
-
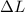 is the change in length (stretch),
is the change in length (stretch),
-
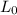 s the original length of the tendon,
s the original length of the tendon,
- Y is Young's modulus,
- A is the cross-sectional area of the tendon.
Given that the force on the Achilles tendon is 8.0 times the runner's weight
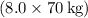 , the force F is
, the force F is
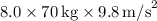 (acceleration due to gravity).
(acceleration due to gravity).
Let's substitute the known values into the formula and solve for
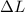 in Part A:
in Part A:
![\[ 8.0 * 70 * 9.8 = (\Delta L)/(0.15 * 10^(10)) * 110 * 10^(-6) \]](https://img.qammunity.org/2020/formulas/physics/high-school/ip5bxxbjcigkupz6zyub72orp8wobdelam.png)
Now, solve for
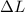 :
:
![\[ \Delta L = ((8.0 * 70 * 9.8) * (0.15 * 10^(10)))/(110 * 10^(-6)) \]](https://img.qammunity.org/2020/formulas/physics/high-school/m9ux9a4pxcvdffdztkzxdqomj8620394v4.png)
Calculate the result to find
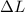 and express it to two significant figures with the appropriate units.
and express it to two significant figures with the appropriate units.
Now, for Part B, calculate the fraction of the tendon's length that corresponds to this stretch:
![\[ \text{Fraction} = (\Delta L)/(L_0) \]](https://img.qammunity.org/2020/formulas/physics/high-school/ndzznz6aq054ijv40q6rgyun93ny890xay.png)
Substitute the values for
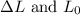 to find the fraction and express it.
to find the fraction and express it.
Let's continue with the calculations.
Part A:
![\[ \Delta L = ((8.0 * 70 * 9.8) * (0.15 * 10^(10)))/(110 * 10^(-6)) \]\[ \Delta L \approx (5488)/(1.1) * 10^4 \]\[ \Delta L \approx 49890 \, \text{m} \]](https://img.qammunity.org/2020/formulas/physics/high-school/609vsm4ikeoqwpo1jwpgceu22r1vsbygyq.png)
Expressed to two significant figures, this is approximately
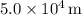 .
.
Part B:
Now, calculate the fraction of the tendon's length:
![\[ \text{Fraction} = (\Delta L)/(L_0) \]](https://img.qammunity.org/2020/formulas/physics/high-school/ndzznz6aq054ijv40q6rgyun93ny890xay.png)
Given that the original length
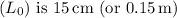 :
:
![\[ \text{Fraction} = (5.0 * 10^4)/(0.15) \]\[ \text{Fraction} \approx 3.33 * 10^5 \]](https://img.qammunity.org/2020/formulas/physics/high-school/7wdslkqk6jx2sa5nx95083zxf4wo9a1rax.png)
Expressed to two significant figures, this is approximately
 .
.
So, the runner's Achilles tendon would stretch by approximately
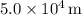 and this corresponds to about
and this corresponds to about
 times the tendon's original length.
times the tendon's original length.