Answer:
a)
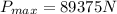
b)

Step-by-step explanation:
a) The maximum load that may be applied to a specimen of bronze alloy without plastic deformation is given by the following equation :
Pmax = (σ).(A)
Where Pmax is the maximum load
σ is the value at which plastic deformation begins
Where ''A'' is the cross-sectional area of the specimen
Let's also use the fact that :

We first must turn ''A'' from
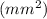 to
to
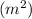
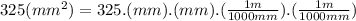
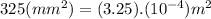
Using the equation :
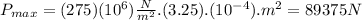
The maximum load is 89375 N.
b) To calculate the maximum length we are going to use the following equation :
Lf = Li ( 1 + σ / E )
Where Lf is final length without causing plastic deformation
Li is initial length
σ is the value at which plastic deformation begins
And finally ''E'' is the modulus of elasticity from the bronze alloy
Using the equation :
