Answer:
The probability of at least one person will catch the flu is 0.5952
Explanation:
To find the probability of al least one catches the flu, we need to find the difference between 1 and the probability of not catching the flu.
The probability of catching the flu varies if the person is inoculated or not.
Let the events be:
E: the person was exposed
F: the person catches the flu
Hence, it is attached a tree diagram of the sample space. According to the diagram:
Inoculated person:
P(F')= 0.6×0.8 + 0.4×1 = 0.88 (We choose the second and the fourth way)
Not inoculated person:
P(F')= 0.6×0.1 + 0.4×1= 0.46 (We choose the second and the fourth way)
Let the events be:
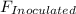 = the person is inoculated and catches the flu
= the person is inoculated and catches the flu
 =the person is not inoculated and catches the flu
=the person is not inoculated and catches the flu
Using complementary events, DeMorgan’s Laws, and independence we have:
P(
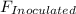 ∪
∪
 )=1-P(
)=1-P(
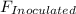 ∪
∪
 )'
)'
=1 - P(
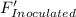 ∩
∩
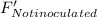 )
)
=1 - P(
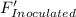 )×P(
)×P(
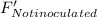 )
)
=1 - (0.88)×(0.46)
=1 - 0.4048
=0.5952
The probability of at least one will catch the flu for a randomly selected person is 0.5952