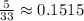Question

Incoming students to a certain school take a mathematics placement exam. The possible scores are 1, 2, 3, and 4. From past experience, the school knows that if a particular student's score is x {1,2,3,4}, then the student will become a mathematics major with probability x-1/x+3 Suppose that the incoming class had the following scores: 10% of the students scored a 1, 20% scored a 2, 60% scored a 3, and 10% scored a 4. What is the probability that a Randomly selected student from the incoming class will become a mathematics major? Express your answer as a fraction in lowest terms. Suppose a randomly selected student from the incoming class turns out to be a mathematics major. What is the probability that she scored a 4 on the placement exam? Express your answer as a fraction in lowest terms.

Answer 1

The probability that a Randomly selected student from the incoming class will become a mathematics major is
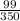`(99)/(350)` or 0.2829

The probability that she scored a 4 on the placement exam is
`(5)/(33)\approx 0.1515`

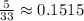
Explanation:

Consider the provided information.

Then, the given student score is:

10% of the students scored a 1 = 10% = 10/100=1/10

20% of the students scored a 2 = 20% = 20/100=2/10

60% of the students scored a 3 = 60% = 60/100=6/10

10% of the students scored a 4 = 10% = 10/100=1/10

The student will become a mathematics major with probability x-1/x+3.

Calculate the probability for x=1,2,3 and 4

Let the event M denote that a randomly selected student will become a math major.

`P(M|x=1)=(x-1)/(x+3)=(1-1)/(1+3)=0`

`P(M|x=2)=(x-1)/(x+3)=(2-1)/(2+3)=(1)/(5)`

`P(M|x=3)=(x-1)/(x+3)=(3-1)/(3+3)=(1)/(3)`

`P(M|x=4)=(x-1)/(x+3)=(4-1)/(4+3)=(3)/(7)`

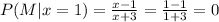
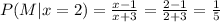
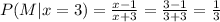
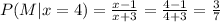
Part (A)

Now calculate the probability that a Randomly selected student from the incoming class will become a mathematics major.

`P(M)=\sum_(i=1)^(4)P(M|x_i)P(x_i)`

`P=(1)/(10)* 0+(2)/(10)* (1)/(5)+(6)/(10)* (1)/(3)+(1)/(10)* (3)/(7)`

`P=(99)/(350)\approx 0.2829`

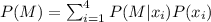
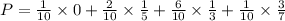
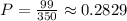
Hence, the probability that a Randomly selected student from the incoming class will become a mathematics major is
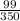`(99)/(350)` or 0.2829

Part (B)

What is the probability that she scored a 4 on the placement exam?

`P(X_4|M)=(P(M|x_4)P(x_4))/(P(M))`

`P(X_4|M)=((3)/(7)\cdot (1)/(10))/((99)/(350))`

`P=(5)/(33)\approx 0.1515`

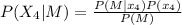
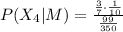
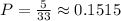
Hence, the probability that she scored a 4 on the placement exam is
`(5)/(33)\approx 0.1515`