Question

The blood type O negative is called the "universal donor" type because it is the only blood type that may safely be transfused into any person. Therefore, when someone needs a transfusion in an emergency and their blood type cannot be determined, they are given type O negative blood. For this reason, donors with this blood type are crucial to blood banks. Unfortunately, this blood type is fairly rare; according to the Red Cross, only 7 percentage of U.S. residents have type O negative blood. Assume that a blood bank has recruited 20 unrelated donors. (State calculator entry and give 4 decimal places) What is the probability that fewer than three of them will have type O negative blood? What is the probability that more than 4 of them have type O negative blood? Find the probability that none of the donors had type O negative blood. Would this be unusual? Explain. What is the mean of the number of donors who have type O negative blood for a group this size? What is the standard deviation of the number of donors who have type O negative blood for a group this size?

Answer 1

Probability that fewer than three of them will have type O negative blood: P(x<3)=0.6047

Probability that more than 4 of them have type O negative blood: P(x>4)=0.0472

Probability that none of the donors had type O negative blood: P(x=0)=0.2342

Mean of the number of donors who have type O negative blood for a group this size: E=1

Standard deviation of the number of donors who have type O negative blood for a group this size: SD=2

Explanation:

These experiments behave as binomial distribution:

P(x)=
`(n!)/(x!(n-x)!). p^x.(1-p)^(n-x)`

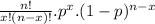
where:

x: donors have type O negative blood

p: success outcome (0.07)

n: unrelated donors (20)

Fewer than three donors will have type O negative blood:

P(x<3)=P(x=0)+P(x=1)+P(x=2)=
`(20!)/(0!(20-0)!). (0.07)^0.(1-0.07)^(20-0)`+
`(20!)/(1!(20-1)!). (0.07)^1.(1-0.07)^(20-1)`+
`(20!)/(2!(20-2)!). (0.07)^2.(1-0.07)^(20-2)}`

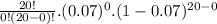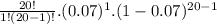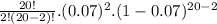
P(x<3)=0.2342+0.3526+0.2521=0.8389

More than 4 of donors have type O negative blood:

P(x>4)=1-P(x<4)= 1 - P(x=0) - P(x=1) - P(x=2) - P(x=3)= 1 - 0.2342 - 0.3526 - 0.2521 - 0.1139=0.0472

None of the donors had type O negative blood:

P(x=0)=
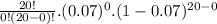`(20!)/(0!(20-0)!). (0.07)^0.(1-0.07)^(20-0)`=0.2342

Mean of the number of donors who have type O negative blood:

E=n×p=20×0.07=1.4≅1

The mean number of donors that have type O negative blood is 1.

Standard deviation of the number of donors who have type O negative blood:

SD=
`√(npq)`=
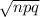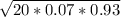`√(20*0.07*0.93)`=1.5≅2

The standard deviation of the distribution of donors that have type O negative blood is 2.