Question

Let A and B be subsets of a universal set U and suppose n(U) = 400, n(A) = 115, n(B) = 90, and n(A ∩ B) = 50. Find the number of elements in the set.

Answer 1

By the inclusion/exclusion principle,

`n(A\cup B)=n(A)+n(B)-n(A\cap B)=155`

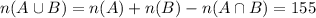
There are 400 elements in the universal set
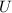`U`, which means there are 400 - 155 = 245 elements not accounted for by
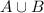`A\cup B`, or

`n(U)=n(A\cup B)+n((A\cup B)^C)\implies n((A\cup B)^C)=245`

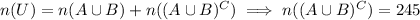
That's all you can really determine from the given info. Considering the language of the problem, "Find the number of elements in the set", I find it hard to believe that the set it's talking about isn't mentioned.