Answer:
0.3723
Explanation:
We are given a system consisting of three independent components.
Let the three components be A , B and C
The lifetimes of these components follow an Exponential distribution with mean 300 hours, 410 hours, and 600 hours, respectively
a) Suppose that the system works only if all three components are functional (e.g., series connection). Find the probability that the system still works after 550 hours.
Exponential Distribution :
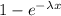
P(A)=P(x>550) =
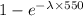
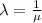
P(A)=P(x>550) =

P(A)=P(x>550) =
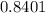
P(B)=P(x>550) =
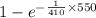
P(B)=P(x>550) =
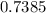
P(C)=P(x>550) =
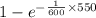
P(C)=P(x>550) =
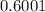
Since P(A) , P(B) , P(C) are independents
So, the probability that all three components still work after 550 hours = P(A)*P(B)*P(C)=

Hence the probability that all three components still work after 550 hours is 0.3723