Answer:
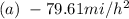
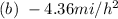
Explanation:
Let's rewrite the equation as:
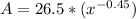
Now, let's find its derivate:
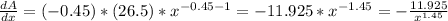
Let's evaluate x=0.27 and x=2:
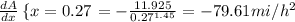
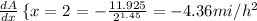
Keep in mind that when we derivate A(average speed) we find the average acceleration, thats why the result is given in mi/h^2, also it explains the minus sign, because for every stop you make on the trip you are decelerating.