Question

The outer surface of an steel alloy is to be hardened by increasing its carbon content. The carbon is to be supplied from an external carbon-rich atmosphere, which is maintained at an elevated temperature. A diffusion heat treatment at 826°C for 10 min increases the carbon concentration to 0.83 wt% at a position 1.3 mm below the surface. Estimate the diffusion time required at 610°C to achieve this same concentration also at a 1.3 mm position. Assume that the surface carbon content is the same for both heat treatments, which is maintained constant. The preexponential and activation energy values for the diffusion of carbon in the iron are 8.3 × 10-8 m2/s and 78.5 kJ/mol, respectively.

Answer 1

Diffusion time needed for 610 degree celcius is 81.91 min

Step-by-step explanation:

Given data:

Diffusion heat temperature = 826 + 273 = 1099 K

Diffusion time t_1 = 10 min

carbon concentration = 0.83%

`D_O = 8.3* 10^(-8)  m^2/s`

`Q_d = 78.5 kJ/kg`

`T_2 = 610+273 = 883 K`

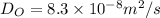
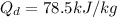
From Fick's formula we hvae

`( C_x - C_o)/(C_z -C_o) = 1 -erf((x)/(2√(Dt))`

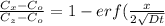
at specific concentration

`( C_x - C_o)/(C_z -C_o) = constant`

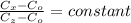
then

`((x)/(2√(Dt)) = constant`

`(\frac{x^2}{{Dt}} = constant`

Dt = constant

`D_1 t_1 = D_2 t_2`

`t_2 = (D_1 t_1)/(D_2)`

`D_1 at T_1`

`D_1 = D_o exp((Q_d)/(R t_1))`

`= 8.3* 10^(-8) exp((78.5* 10^3)/(8.314 * 1099))`

`= 1.54* 10^(-11) m^2/s`

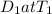
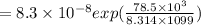
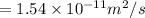
similarly for D_2 for T_2

`D_2 = 1.88* 10^(-12) m^2/s`

`t_2 = (D_1 t_1)/(D_2)`

`= (1.54* 10^(-11) * 10)/(1.88* 10^(-11))`

`t_2    = 81.91 min`

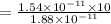
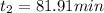
Diffusion time needed for 610 degree celcius is 81.91 min