Answer:
Meter marks are on cut-off portion of stick is 100 - 60 = 40 m
Step-by-step explanation:
Given data:
Spaceship length of L = 100 m
Relative velocity between the ship and stick is given as
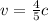
The observed length observed by the outside observer is
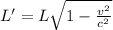
putting all value to get observe length
put
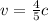
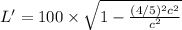
L' = 60 m
Meter marks are on cut-off portion of stick is 100 - 60 = 40 m