Question

The variable a is the length of the ladder. The variable h is the height of the ladder's top at time t, and x is the distance from the wall to the ladder's bottom. Suppose that the length of the ladder is 5.0 meters and the top is sliding down the wall at a rate of 0.4 m/s. Calculate dx dt when h = 3.1.

Answer 1

`(dx)/(dt)` = 0.3

Explanation:

The given situation forms a right triangle. We have to use the Pythagorean theorem's statement to solve this problem.

The theorem states that the sum of the squares of the legs is equal to the square of the hypotenuse.

Here Hypotenuse = length of the ladder (a)

Legs are h and x.

So, using the Pythagorean theorem, we get

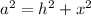`a^2 = h^2 + x^2` -------------(1)

We are given a = 5 meters,
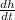`(dh)/(dt)` = 0.4

Now plug in a = 5 in the above equation, we get

`5^2 = h^2 + x^2`

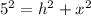
25 =
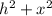`h^2 + x^2` -----(2)

To find the
`(dx)/(dt)` . Differentiate the above equation with respective to the time t, we get

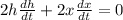`2h(dh)/(dt) + 2x(dx)/(dt) = 0\\` -------(3)

We know that h = 3.1 and
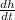`(dh)/(dt)` = 0.4.

We can find x, by plug in h = 3.1 from the equation (2)

25 =
`3.1^2 + x^2`

`x^2 = 25 - 9.61`

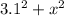
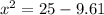
x = 3.9

Now plug h = 3.1, x = 3.9 and
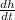`(dh)/(dt)` = -0.4 in the derivative (3) and find dx/dt

Here we represents
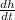`(dh)/(dt)` = -0.4 because it is sliding down

2(3.1)(-0.4) + 2(3.9)
`(dx)/(dt)` = 0

-2.48 + 7.8
`(dx)/(dt)` = 0

7.8
`(dx)/(dt)` = -2.48

`(dx)/(dt)` = -2.48 ÷ -7.8

`(dx)/(dt)` = 0.3179

When we rounding off to the nearest tenths place, we get

`(dx)/(dt)` = 0.3

Answer 2

dx/dt= 0.2608 at h= 3.1 m

Explanation:

a is the length of the ladder. a=5

by pythagorus theorem

`x^2 = a^2-h^2`

differentiating with respect to t we get

`x(dx)/(dt) = -h(dh)/(dt)`......1

The variable h is the height of the ladder's top at time t, and x is the distance from the wall to the ladder's bottom

At h= 3.1

x^2= 6^2-3.1^2 = 9.1×2.9

x= 5.1371 m

given
`(dh)/(dt) =-0.4`

putting values in 1 to get dx/dt

`5.1371(dx)/(dt) = 3.1×04`.

dx/dt= 0.2608 at h= 3.1 m