Answer:
There is a 6.01% probability that a randomly selected person aged 40 years or older is a female and jogs.
It would not be unusual to randomly select a person aged 40 years or older who is a female and jogs.
Explanation:
We have these following probabilities:
A 26.6% probability that a randomly selected person aged 35 years or older is a jogger, so
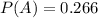 .
.
A 22.6% probability that a randomly selected person aged 35 years or older is female, given that he or she jogs. I am going to say that P(B) is the probability that the person is a female. P(B/A) is the probability that the person is a female, given that he/she jogs. So
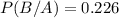 .
.
The Bayes theorem states that:

In which
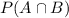 is the probability that the person does both thigs, so, in this problem, the probability that a randomly selected person aged 40 years or older is a female and jogs.
is the probability that the person does both thigs, so, in this problem, the probability that a randomly selected person aged 40 years or older is a female and jogs.
So

There is a 6.01% probability that a randomly selected person aged 40 years or older is a female and jogs.
A probability is unusual when it is smaller than 5%.
So it would not be unusual to randomly select a person aged 40 years or older who is a female and jogs.