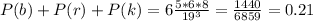Question

Poker chips are added to a hat: 5 blue, 6 red, and 8 black. If a set of 3 chips is randomly selected without replacement, what is the probability that each of the chips will be

(1) of the same color
(2) of different colors?
What is the answer to (1) and (2) if after selection of each individual chip, it is noted and then returned to the hat?

Answer 1

Without replacement:

(1) P =0.0888

(2) P=0.248

With replacement:

(1) P=0.1244

(2)P=0.21

Explanation:

There is a total of 5+6+8=19 balls. The probability of 3 picks being the same color is the sum of the probability of them being all blue P(b) plus the probability of them being all red P(r), and the probability of them all being black P(k).

`P(b)=(5)/(19)*(4)/(18)*(3)/(17)=(60)/(5814)=0.01032`

`P(r)=(6)/(19)*(5)/(18)*(4)/(17)=(120)/(5814)=0.02064`

`P(k)=(8)/(19)*(7)/(18)*(6)/(17)=(336)/(5814)=0.0578`

`P(b)+P(r)+P(k)=0.0888`

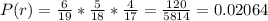
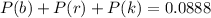
The possibilities for them to be of different colors are:

brk, bkr, rbk, rkb, kbr, krb

The probability of them being of different colors is the sum of those probabilities. Since they are all equally likely:

`P=6*(5)/(19)*(6)/(18)*(8)/(17)=(1440)/(5814)=0.248`

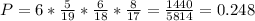
With replacement, we have for (1):

`P(b)=(5)/(19)*(5)/(19)*(5)/(19)=((5)/(19))^3=0.0182`

`P(r)=((6)/(19))^3=0.0315`

`P(k)=((8)/(19))^3=0.0746`

`P(b)+P(r)+P(k)=.01244`

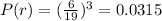
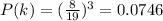
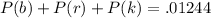
and for (2):

`P(b)+P(r)+P(k)=6(5*6*8)/(19^3)=(1440)/(6859)=0.21`