Answer:
t = 56.6 min
Step-by-step explanation:
Fick's second law is used to calculate time required for diffusion
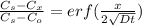
where
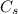 = 1.15%
= 1.15%
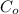 = 0.18%
= 0.18%
 = 0.35%
= 0.35%
x = 0.40 mm = 0.0004 n
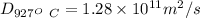
therefore we ahave
![(1.15-0.35)/(1.15- 0.18) = erf[\frac{4* 10^(-4)}{2\sqrt{1.28* 10^(-11) t}}]](https://img.qammunity.org/2020/formulas/engineering/college/khcz6th63cuojij9xfq5kzz1t161n39xoc.png)
![0.8247 = erf [(55.90)/(√(t))] = erf z](https://img.qammunity.org/2020/formulas/engineering/college/q6xn9lv7501b0seviovx87qzucbbr0hm1k.png)
from error function table we hvae following result
for erf z z
0.8209 0.95
0.8247 x
0.8427 1
therefore
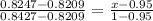
x = 0.959
thus


t = 56.6 min